¡Hola! Hoy vamos a hablar de una figura geométrica que, aunque parece sencilla, tiene propiedades fascinantes: el rombo. ¿Alguna vez te has preguntado qué es un rombo? Imagina un cuadrado que ha sido estirado en un ángulo. Eso es, en esencia, un rombo. A diferencia de un cuadrado, donde todos los ángulos son rectos, en el rombo los ángulos son oblicuos, pero todos sus lados son iguales. Una de las características más interesantes de esta figura son sus diagonales. En este artículo, nos centraremos especialmente en la diagonal mayor del rombo, su cálculo, propiedades y por qué es tan importante. Así que, si estás listo, ¡vamos a sumergirnos en el mundo del rombo!
¿Qué es un Rombo?
Antes de hablar de la diagonal mayor, es esencial entender bien qué es un rombo. Un rombo es un cuadrilátero con todos sus lados de la misma longitud. Piensa en un diamante: tiene esa forma característica que todos reconocemos. Pero no solo se trata de la forma, sino también de las propiedades. Por ejemplo, los ángulos opuestos son iguales, y las diagonales se cruzan en un ángulo recto, dividiéndose mutuamente en partes iguales. Esto último es crucial cuando hablamos de las diagonales, así que no lo olvides.
Las Diagonales del Rombo
En un rombo, hay dos diagonales: la diagonal mayor y la diagonal menor. La diagonal mayor es la más larga de las dos y se extiende de un vértice a otro que no está adyacente. Por otro lado, la diagonal menor conecta los otros dos vértices. ¿Te imaginas un rombo como una cometa? Las diagonales son como las varillas que sostienen la cometa, formando la estructura. Pero, ¿por qué son tan importantes? Las diagonales no solo ayudan a definir la forma, sino que también son clave para calcular el área y otras propiedades del rombo.
Cálculo de la Diagonal Mayor
Ahora que tenemos una idea básica del rombo y sus diagonales, hablemos de cómo calcular la diagonal mayor. La fórmula básica para encontrar la diagonal mayor (D) en función de los lados (a) y la diagonal menor (d) es la siguiente:
D = √(4a² – d²)
¿Te parece complicada? No te preocupes, vamos a desglosarla. Supongamos que tienes un rombo con lados de 5 cm y una diagonal menor de 4 cm. Primero, elevarías 5 al cuadrado, lo que te da 25, y luego multiplicas eso por 4, lo que da 100. Luego, elevas 4 al cuadrado, que es 16, y lo restas de 100. Al final, obtienes 84. Si sacas la raíz cuadrada de 84, obtienes aproximadamente 9.17 cm. ¡Y ahí tienes tu diagonal mayor!
Propiedades de la Diagonal Mayor
La diagonal mayor no es solo un número; tiene propiedades fascinantes. Una de las más importantes es que, como mencionamos antes, divide el rombo en dos triángulos congruentes. Esto significa que ambos triángulos tienen la misma área y forma. Además, la diagonal mayor es siempre más larga que la diagonal menor, lo que crea una especie de equilibrio en la figura. Si piensas en un rombo como un balancín, la diagonal mayor sería la parte más larga que ayuda a mantener todo en equilibrio.
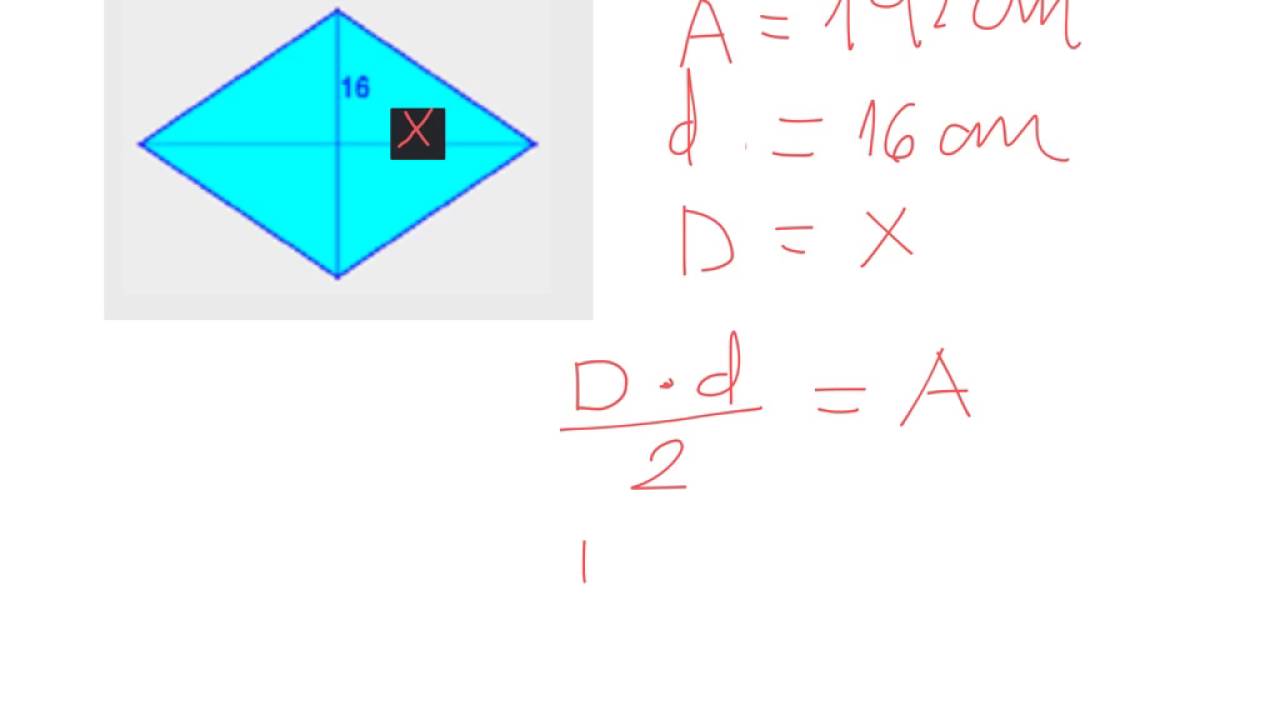
Relación con el Área del Rombo
La diagonal mayor también está relacionada con el cálculo del área del rombo. La fórmula para calcular el área (A) de un rombo es:
A = (D * d) / 2
Donde D es la diagonal mayor y d es la diagonal menor. Esto significa que, si conoces una diagonal y el área, puedes calcular la otra diagonal. Por ejemplo, si el área de tu rombo es 20 cm² y la diagonal menor es 4 cm, puedes reorganizar la fórmula para encontrar la diagonal mayor. Simplemente multiplicas 20 por 2 y lo divides por 4, lo que te da 10 cm como resultado para la diagonal mayor. ¡Así de sencillo!
Ejemplos Prácticos
Para que todo esto sea más claro, veamos algunos ejemplos prácticos. Supongamos que tienes un rombo con lados de 6 cm y una diagonal menor de 5 cm. Usando nuestra fórmula para la diagonal mayor:
D = √(4(6)² – (5)²)
Esto se convierte en D = √(144 – 25), lo que nos da D = √119, que es aproximadamente 10.91 cm. Así que, en este caso, tu diagonal mayor sería de 10.91 cm.
¿Qué pasa si solo tienes la Diagonal Mayor?
¡Buena pregunta! Si solo tienes la diagonal mayor y quieres encontrar la diagonal menor, puedes reorganizar la fórmula inicial. Digamos que tienes una diagonal mayor de 12 cm y lados de 7 cm. La fórmula se convierte en:
d = √(4(7)² – (12)²)
Esto se convierte en d = √(196 – 144), que resulta en d = √52, o aproximadamente 7.21 cm. Así que, ¡ahí lo tienes!
Aplicaciones Prácticas del Rombo
Ahora que ya sabes cómo calcular la diagonal mayor y sus propiedades, es interesante ver cómo se aplican en la vida real. Los rombos no son solo figuras matemáticas; los encontramos en el diseño de joyas, en la arquitectura e incluso en la naturaleza. Por ejemplo, los paneles de vidrio en algunas estructuras pueden tener forma de rombo, y los patrones en la naturaleza, como en ciertas hojas, a menudo reflejan esta forma.
El Rombo en el Arte y la Arquitectura
En el mundo del arte y la arquitectura, el rombo se utiliza para crear patrones y simetrías. ¿Alguna vez has visto un mosaico? Muchos de ellos incorporan rombos en sus diseños, creando una estética visualmente atractiva. Además, en arquitectura, los rombos pueden ser utilizados para maximizar el espacio y la luz en una habitación, gracias a sus diagonales que permiten una distribución única de los elementos.
¿Puedo encontrar la diagonal mayor si solo tengo los lados del rombo?
Sí, si conoces la longitud de los lados, puedes calcular la diagonal mayor siempre que también tengas la diagonal menor. Necesitarás ambas medidas para aplicar las fórmulas correctamente.
¿Las diagonales de un rombo siempre se cruzan en un ángulo recto?
¡Exactamente! Una de las propiedades más fascinantes de las diagonales de un rombo es que se cruzan en un ángulo de 90 grados, dividiendo el rombo en cuatro triángulos rectángulos.
¿Cómo se relacionan las diagonales con el perímetro del rombo?
Las diagonales no afectan directamente el perímetro del rombo, ya que el perímetro se calcula solo con la longitud de los lados. Sin embargo, las diagonales son fundamentales para entender la forma y las propiedades del rombo.
¿El rombo tiene alguna aplicación en la vida cotidiana?
Definitivamente. Los rombos son comunes en el diseño de objetos, en la arquitectura, en patrones de tela y en la naturaleza. Su forma única y equilibrada los hace visualmente atractivos y funcionales.
¿Puedo usar la diagonal mayor para calcular la altura del rombo?
Sí, la diagonal mayor se puede utilizar junto con la diagonal menor para calcular la altura del rombo mediante la relación entre las áreas de los triángulos formados por las diagonales.
Y ahí lo tienes, un recorrido completo por el mundo del rombo y su diagonal mayor. Esperamos que te haya resultado útil y que ahora tengas una mejor comprensión de esta figura geométrica. ¿Tienes alguna otra pregunta? ¡Déjanos un comentario!