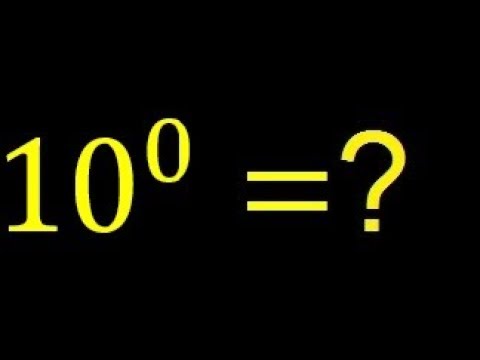¿Te has preguntado alguna vez qué ocurre cuando elevamos un número a la potencia cero? Parece una pregunta sencilla, pero la respuesta, aunque simple, encierra una lógica matemática fascinante que puede no ser inmediatamente intuitiva. A primera vista, podría parecer que 100 es igual a 0, o incluso que no tiene sentido. Sin embargo, la respuesta es 1. Pero ¿por qué? En este artículo, exploraremos la razón detrás de esta regla matemática aparentemente peculiar, desentrañando el misterio del exponente cero y su importancia en el mundo de las matemáticas.
Explorando el Misterio del Exponente Cero
Vamos a desentrañar este enigma paso a paso. Imagina que tienes 103. Esto significa 10 x 10 x 10 = 1000, ¿cierto? Ahora, vamos disminuyendo el exponente: 102 = 10 x 10 = 100; 101 = 10. Observa el patrón: cada vez que reducimos el exponente en 1, dividimos el resultado anterior entre 10. Siguiendo esta lógica, ¿qué ocurre cuando pasamos de 101 a 100? ¡Simple! Dividimos 10 entre 10, lo que nos da 1.
La Lógica de la Divison
Piensa en ello como una secuencia de divisiones. Si tenemos 103, para llegar a 102 dividimos entre 10. Para llegar a 101, volvemos a dividir entre 10. Para llegar a 100, la lógica nos dicta que debemos dividir una vez más entre 10. 10 dividido entre 10 es 1. Así, manteniendo la consistencia de la operación, 100 = 1. No es una regla arbitraria, sino una consecuencia natural de la definición de la exponenciación.
Más allá de 10: Generalizando la Regla
Este principio no se limita únicamente al número 10. Funciona para cualquier número real (excepto el cero, como veremos más adelante). Por ejemplo, 50 = 1, 20 = 1, (-3)0 = 1, y así sucesivamente. La regla es universal: cualquier número (excepto 0) elevado a la potencia cero es igual a 1. Es una propiedad fundamental del sistema numérico.
¿Por qué no se puede elevar 0 a la potencia 0?
Aquí es donde las cosas se ponen interesantes. El caso de 00 es un caso especial y no está definido en matemáticas. ¿Por qué? Porque si intentamos aplicar la lógica de la división, nos encontramos con un problema. Si seguimos el patrón de reducir el exponente, tendríamos 01 = 0, 02 = 0, etc. Si seguimos este patrón, ¿qué ocurre cuando bajamos a 00? Dividir 0 entre 0 es una operación indefinida, ya que no hay un resultado único y consistente. Es como preguntar: «¿Cuántos ceros caben en un cero?» La pregunta no tiene sentido.
La perspectiva del límite
Desde la perspectiva del cálculo, podemos aproximarnos al concepto de 00 usando límites. Sin embargo, el límite de xy cuando x y y tienden a 0 depende del camino por el que nos aproximamos a 0. Esto significa que el resultado puede variar, lo que refuerza la idea de que 00 no tiene un valor definido. Es una indeterminación.
Aplicaciones del Exponente Cero
Aunque pueda parecer una regla matemática abstracta, el exponente cero tiene aplicaciones prácticas en diversos campos. En álgebra, es crucial para simplificar expresiones y resolver ecuaciones. En cálculo, juega un papel importante en el estudio de funciones y límites. En informática, se utiliza en algoritmos y análisis de datos. Su aparente sencillez esconde una profunda importancia en el desarrollo de las matemáticas modernas.
Ejemplos en la vida real (o casi)
Piensa en la probabilidad. Si tienes una bolsa con 10 canicas, y quieres calcular la probabilidad de sacar una canica roja, sabiendo que no hay canicas rojas, la probabilidad es 0/10 = 0. Ahora, ¿cuál es la probabilidad de sacar una canica que *no* sea roja? Es 10/10 = 1, o 100%. Puedes ver cómo el concepto de «ninguna canica roja» se relaciona con el exponente cero, aunque no de manera directa.
Más allá de los Números
La idea del exponente cero se extiende más allá de los números. En la teoría de conjuntos, el conjunto vacío tiene 0 elementos. Si consideramos el número de subconjuntos del conjunto vacío, este es 1 (el conjunto vacío mismo). Esto se relaciona con la idea de que 00 (aunque indefinido numéricamente) podría interpretarse como 1 en un contexto diferente.
En resumen, aunque parezca contraintuitivo, cualquier número (excepto 0) elevado a la potencia cero es igual a 1. Esta regla no es arbitraria, sino una consecuencia lógica de las propiedades de la exponenciación y la división. El caso de 00 es una excepción, ya que es una indeterminación matemática. A pesar de su aparente sencillez, el exponente cero juega un papel fundamental en diversas áreas de las matemáticas y sus aplicaciones.
¿Por qué 0 elevado a 0 no está definido?
0 elevado a 0 es indefinido porque la operación de dividir 0 entre 0 no tiene un resultado único y consistente. Los intentos de definirlo mediante límites conducen a resultados contradictorios dependiendo del camino de aproximación.
¿Existen otras excepciones a la regla del exponente cero?
No, la única excepción es 0 elevado a 0. Para cualquier otro número real, la regla se cumple: el número elevado a 0 es igual a 1.
¿Cómo puedo explicar esto a alguien que no entiende de matemáticas?
Puedes usar la analogía de las divisiones sucesivas. Si tienes 10 canicas y las vas dividiendo en grupos de 10, primero tendrás 1 grupo de 10, luego 1 grupo de 1, y si intentas dividir ese último grupo en 10, tendrás 0 grupos de 10 canicas, pero ese 1 grupo que te queda representa el 1 que obtienes al elevar 10 a la 0.
¿Tiene alguna aplicación práctica el concepto de 0 elevado a 0?
Aunque 0 elevado a 0 no está definido, el concepto subyacente de indeterminación es importante en el análisis matemático y en el estudio de límites. En ciertos contextos, se puede asignar un valor convencional para facilitar el trabajo, pero siempre se debe tener en cuenta su indeterminación.
¿Es importante entender el concepto del exponente cero?
Sí, es fundamental para comprender las bases del álgebra, el cálculo y otras ramas de las matemáticas. Dominar este concepto simplifica la resolución de ecuaciones y el análisis de funciones.